やねうら王搭載の詰将棋ルーチンの千日手対応
Qhapaq アドベント将棋記事 14日目
やねうら王(tnk-)に搭載のdf-pnベースの詰将棋エンジンが図巧の1番を解けないことが発覚しました。時折聞かれる「コム将棋の開発ってどうやってやるの」という問への答えとして使えそう課題なので、図巧の1番の解決を目指したライブデバッギングをネタの水増しとしてやっていきたいと思います。
【1日目】
【まずどの局面で詰まないのかを二分探索する】
図巧の答えを見たい人はこちら。
図巧の1番は69手目という超大作です。詰むはずの局面を詰まないと言われただけで問題が見えるレベルのサイズではありません。というわけで、まずは2分探索をして、何手目から読ませたら詰まなくなるのかを確かめます。
30手目から...詰む
16手目から...詰む
8手目から...詰まない
12手目から...詰まない
14手目から...詰む
ということで、どうやら13手目に対して不詰の変化がある(模範解答は14手目が正確ではない)と主張していることが解りました。


となると、13手目の15飛車打に対して、tnkの詰め将棋ルーチンはどんな手で詰まないと主張しているかを知るのが良さそうなことが解ります。打ち歩詰めや合法手生成が間違っているのか、はたまた本当に不詰なのか......
【2日目】
【詰まない変化を追いかける】
次にやねうら王を改造し、不詰の局面でどのような変化を提案するかを調べます。不詰の変化を全列挙するのは大変なので、特定の変化(手順をmove形式で与える)についてのみ、ハッシュテーブルに保存されたpn、dnをとりだせるようにした上で、詰みの場合は詰みの手を、不詰の場合は不詰の手を返すようにします。
その結果、13手目から探索をした場合▲15飛車打、14手目△25飛車打の手順が不詰である(▲15飛車打、14手目△25飛車打したあとの局面を初期局面にした場合は詰むにもかかわらず!)という出力が得られました。
となれば、何かしかの影響で、詰み手順の中の局面が不当に不詰に書き換えられていると予想できます。
【ハッシュの重複を探す】
局面の評価を書き換えうる要素としてまず浮かぶのが局面のハッシュ(キー)の重複です。この詰め将棋エンジンではキーは32bitであるため、億単位の局面を探索すれば重複がありえます。幸いにも、上述の「詰まない」と言われる局面で探索される局面の数は数千万オーダーなので、局面のsfen文字列を全て保持してもメモリは爆発しなさそうです。
そこで、局面が新しく探索されるたびに、その局面のハッシュとsfenのペアを保存し、異なる局面が同じハッシュを持っていないかをチェックしました(mapでデータを扱えば局面数をNとした場合の計算量はO(NlogN)なので全ての組み合わせについて検証が可能です)。ところが、局面のハッシュ衝突は見られませんでした。となると、少なくとも今回の問題ではハッシュ衝突は原因ではないようです。
【千日手の処理がどうやらおかしいようだ】
ハッシュが原因ではないということで、不詰にされた局面をよく眺めると、どうやら千日手周りの局面で評価がおかしいことに気付きました。tnkの詰め将棋エンジンでは千日手になった局面は不詰の評価を付けていますが間違いです。というのも、「千日手の変化は不詰」であっても「千日手の変化の途中で出てくる局面が不詰」とは限らないからです。例えば以下のような局面で千日手の筋が見つかったことを理由にこれらの局面を不詰にすると、本当は詰む問題について詰まないという結論が出てしまいます。

【問題の要件をまとめる】
千日手周りの問題を処理するには以下の要件を満たす必要があります。
・何らかの理由で千日手周りの変化の検討を打ち切る
・千日手を構成する局面のpn、dnを不当に不詰に変えてしまわない
【3日目】
【千日手処理を書き換える】
問題の要件と今回用いた解決方法を改めて図にまとめると以下のようになります。従来のルーチンでは千日手になった局面を詰まないとみなしていたため、左図のような変化で詰みを見つけることが出来ません。そこで、今回の改造では「千日手の変化で不詰とするのは千日手の変化の中でもっとも開始局面から遠い局面(末端局面)とする」、「末端局面が攻め手側の場合は、親局面に戻る手を違法とする」ことで今まで扱えなかった変化で詰み筋を見つけられるようにしました。

【以下、感想戦】
【原著論文の実装しょぼくね?】
原著論文の実装ではこんなありがちなケースも解けないのか、と思うかも知れませんが、通常の千日手の変化であれば、局面をそもそもループなどせず、攻め手側が別の手を探索してくれます。というのも、普通であれば局面を深く探索するほど局面のpn、dnは増えるため、ループをする時点で親局面や兄弟局面のpnを千日手の変化のpnが上回るからです。
今回の千日手で厄介だったのは受け手側に千日手を拒否する選択権がなかった(王手に対して合法手が1つしかなかった)ことです。これだと手を何度ループしてもpnは1から増えない(pn=1は詰みを除けば最も魅力的な変化)ため、攻め手側も千日手の変化を望んでしまうのです。
【問題は完全解決したのか】
ぶっちゃけしてないと思います。あくまで変な不詰が出る変化が少し減っただけと言えましょう。上記改造の脆弱性としては、例えば、千日手を構成する各々の局面の初期局面からの距離が探索の過程で変わる(より短い手数でその局面にたどり着く方法が見つかる)などがありえます。
【以下、個人的ポエム】
連休を詰将棋の改良に使った感想は「詰将棋の解析は1日でならない」というものでした。やねうら王に搭載されている詰将棋ルーチンの原著論文では、千日手周りの処理についての解説は殆どなく、千日手の処理は「不詰判定の一部」とみなしているようです(恐らく、論文通りの実装した結果が上記の脆弱性なので、解説を端折ってるか論文のやり方に不備があるかだと思います。正直な話、今回考えたハックを原著論文の技術を正しく実装しただけと言われたらちょっとムカつく)。
詰将棋界隈にはまだまだ上がおり、超難しい詰将棋を安定して解かせるという意味では、脊尾詰やなのは詰めのほうがまだまだ格上なのではと正直思います。とはいえ、やねうら王には詰将棋以外のルーチンも搭載されていること、ごく一部の難しい詰将棋でなければ現状の実装でも十分解けること、計算事態が高速であること、オープンソースであり様々な環境で動くこと(個人的にはこれが一番大事)などを考えれば不完全であっても十分な価値があり、一歩ずつでも品質を高めていくのは大事なのではないかなと思います。
今回作ったデバッグ用のコードの中では、詰め将棋探索後にユーザが特定の局面を指定することで、その局面のpn/dnを見られるルーチンは便利だなと思いました。詰将棋エンジンの隠しコマンドとしてコイツもプルリクしたいところです。
【おまけ】
なのは詰めなどの既存ルーチンがwindowsでしか動かないバイナリでしか配られていないと言った所、linuxで動かす方法を色々教えてもらいました。皆様ありがとうございます。
暫く日記の更新が滞ってましたが、手強い問題解決のコツの一つに、気がめいらないように休憩をちょくちょく入れるというのもありますのでそういうことで......
やねうら王搭載の詰将棋ルーチンの改造中継(ver 2)
Qhapaq アドベント将棋記事 13日目
前回の記事もマージしています。
やねうら王(tnk-)に搭載のdf-pnベースの詰将棋エンジンが図巧の1番を解けないことが発覚しました。時折聞かれる「コム将棋の開発ってどうやってやるの」という問への答えとして使えそう課題なので、図巧の1番の解決を目指したライブデバッギングをネタの水増しとしてやっていきたいと思います。
【1日目】
【まずどの局面で詰まないのかを二分探索する】
図巧の答えを見たい人はこちら。
図巧の1番は69手目という超大作です。詰むはずの局面を詰まないと言われただけで問題が見えるレベルのサイズではありません。というわけで、まずは2分探索をして、何手目から読ませたら詰まなくなるのかを確かめます。
30手目から...詰む
16手目から...詰む
8手目から...詰まない
12手目から...詰まない
14手目から...詰む
ということで、どうやら13手目に対して不詰の変化がある(模範解答は14手目が正確ではない)と主張していることが解りました。


となると、13手目の15飛車打に対して、tnkの詰め将棋ルーチンはどんな手で詰まないと主張しているかを知るのが良さそうなことが解ります。打ち歩詰めや合法手生成が間違っているのか、はたまた本当に不詰なのか......
【2日目】
【詰まない変化を追いかける】
次にやねうら王を改造し、不詰の局面でどのような変化を提案するかを調べます。不詰の変化を全列挙するのは大変なので、特定の変化(手順をmove形式で与える)についてのみ、ハッシュテーブルに保存されたpn、dnをとりだせるようにした上で、詰みの場合は詰みの手を、不詰の場合は不詰の手を返すようにします。
その結果、13手目から探索をした場合▲15飛車打、14手目△25飛車打の手順が不詰である(▲15飛車打、14手目△25飛車打したあとの局面を初期局面にした場合は詰むにもかかわらず!)という出力が得られました。
となれば、何かしかの影響で、詰み手順の中の局面が不当に不詰に書き換えられていると予想できます。
【ハッシュの重複を探す】
局面の評価を書き換えうる要素としてまず浮かぶのが局面のハッシュ(キー)の重複です。この詰め将棋エンジンではキーは32bitであるため、億単位の局面を探索すれば重複がありえます。幸いにも、上述の「詰まない」と言われる局面で探索される局面の数は数千万オーダーなので、局面のsfen文字列を全て保持してもメモリは爆発しなさそうです。
そこで、局面が新しく探索されるたびに、その局面のハッシュとsfenのペアを保存し、異なる局面が同じハッシュを持っていないかをチェックしました(mapでデータを扱えば局面数をNとした場合の計算量はO(NlogN)なので全ての組み合わせについて検証が可能です)。ところが、局面のハッシュ衝突は見られませんでした。となると、少なくとも今回の問題ではハッシュ衝突は原因ではないようです。
【千日手の処理がどうやらおかしいようだ】
ハッシュが原因ではないということで、不詰にされた局面をよく眺めると、どうやら千日手周りの局面で評価がおかしいことに気付きました。tnkの詰め将棋エンジンでは千日手になった局面は不詰の評価を付けていますが間違いです。というのも、「千日手の変化は不詰」であっても「千日手の変化の途中で出てくる局面が不詰」とは限らないからです。例えば以下のような局面で千日手の筋が見つかったことを理由にこれらの局面を不詰にすると、本当は詰む問題について詰まないという結論が出てしまいます。

【問題の要件をまとめる】
千日手周りの問題を処理するには以下の要件を満たす必要があります。
・何らかの理由で千日手周りの変化の検討を打ち切る
・千日手を構成する局面のpn、dnを不当に不詰に変えてしまわない
今回は此処まで。
次回はこれらの要件を満たす千日手の処理方法を考えます(次回が最終回です。問題は(多分)解けます)
【おまけ】
なのは詰めなどの既存ルーチンがwindowsでしか動かないバイナリでしか配られていないと言った所、linuxで動かす方法を色々教えてもらいました。皆様ありがとうございます。
暫く日記の更新が滞ってましたが、手強い問題解決のコツの一つに、気がめいらないように休憩をちょくちょく入れるというのもありますのでそういうことで......
今の詰将棋ルーチンが図巧の1番を解けない話
Qhapaqアドベント将棋記事12日目(深夜34時にお送りします)
前々回の記事で解説したdf-pnベースの詰め将棋ルーチンですが、やねうら王(tnk)に搭載されているdf-pnベースのルーチンで図巧(江戸時代に作られたクッソ難しい詰将棋集)の1番が解けないことが発覚しました。時折聞かれる「コム将棋の開発ってどうやってやるの」という問への答えとして使えそう課題なので、ここから暫くは図巧の1番の解決を目指したライブデバッギングをネタの水増しとしてやりたいと思います。
図巧第1番とか pic.twitter.com/bWUljBBFDs
— かず (@kazu_nanoha) 2020年7月21日
ご報告いただいた、かずさん(なのはの中の人)にお礼申し上げます。
【まずどの局面で詰まないのかを二分探索する】
図巧の答えを見たい人はこちら。
図巧の1番は69手目という超大作です。詰むはずの局面を詰まないと言われただけで問題が見えるレベルのサイズではありません。というわけで、まずは2分探索をして、何手目から読ませたら詰まなくなるのかを確かめます。
30手目から...詰む
16手目から...詰む
8手目から...詰まない
12手目から...詰まない
14手目から...詰む
ということで、どうやら13手目に対して不詰の変化がある(模範解答は14手目が正確ではない)と主張していることが解りました。


となると、13手目の15飛車打に対して、tnkの詰め将棋ルーチンはどんな手で詰まないと主張しているかを知るのが良さそうなことが解ります。打ち歩詰めや合法手生成が間違っているのか、はたまた本当に不詰なのか......
今日はここまで。次回は詰め将棋ルーチンを改造して不詰の変化を出力できるようにする....できるといいなあ。
【細かい補足】
ハッシュテーブルが品切れになって盤面の評価が不適切になっている可能性も調査当初はありましたが、ハッシュサイズを変えながら二分探索をすることで、その可能性は低いことも示せました。問題の分割、大事です。
高速な詰将棋アルゴリズムを完全に理解したい(完成版)
Qhapaq アドベント将棋記事10日目
今の詰将棋アルゴリズムで最強と言われているハッシュテーブル+df-pn探索(depth first - proof number)による詰将棋アルゴリズムの完全理解を目指していきます。
参考文献: memo.sugyan.com
【proof numberとは】 proof numberとは平たく言えば詰将棋専用の盤面評価値みたいなものです。通常の盤面評価値と違って、詰み証明のための評価値(pn)と不詰証明のための評価値(dn)があります。pn、dnは「この局面の詰み(proof number)/不詰(disproof number)を証明する為に調べなければならない局面の数」であり、値が小さいほど詰み/不詰に近いという扱いになります。そして、詰み /不詰が証明された局面についてはpn、dnは0になります。局面のpn、dn(厳密には非0のpn、dn)はあくまで探索途中での予測値にすぎないことに注意してください。即ち、pn、dnは探索の途中で増えたり減ったりします。
【ハッシュテーブルとは】 雑に言えば局面毎のpn、dnを保存する辞書のようなものです。将棋などのゲームでは手順前後により重複した局面が多々でてくるため、一度探索した局面を覚えておくことで計算の効率を向上させます。
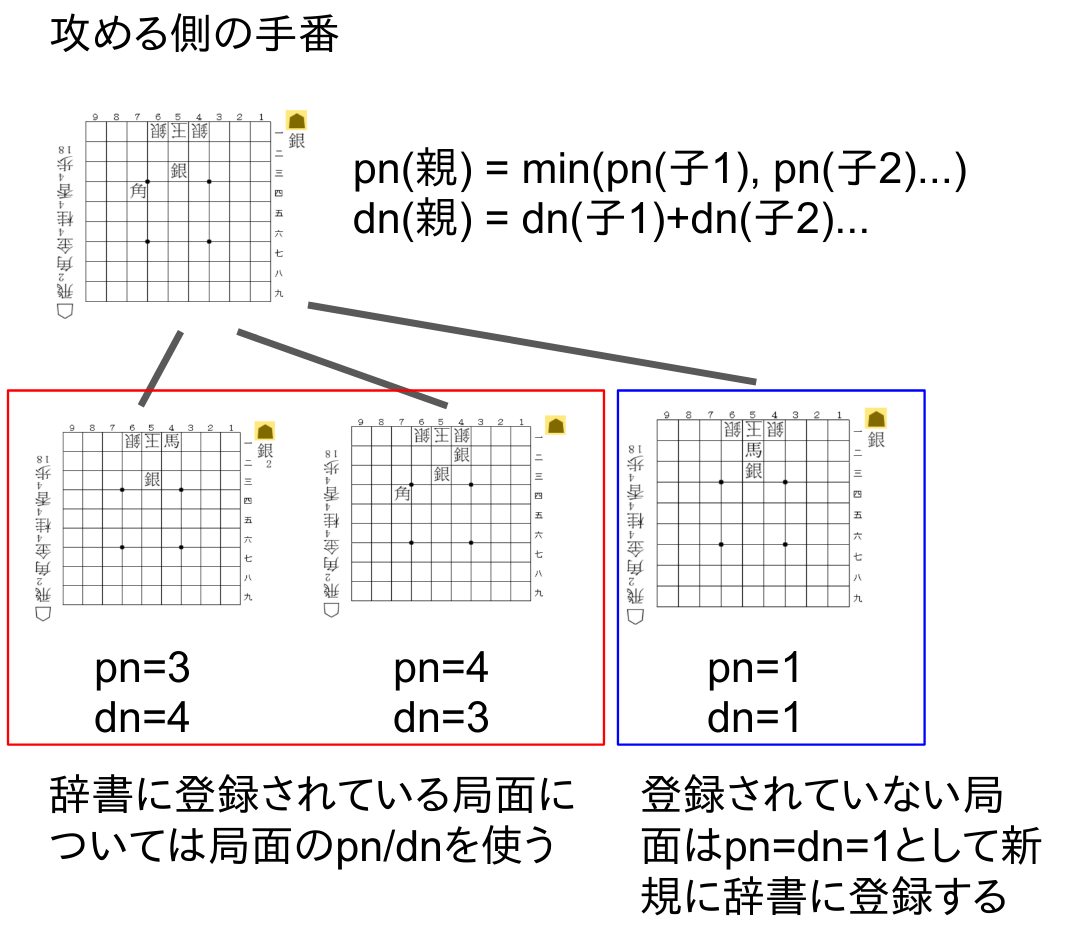
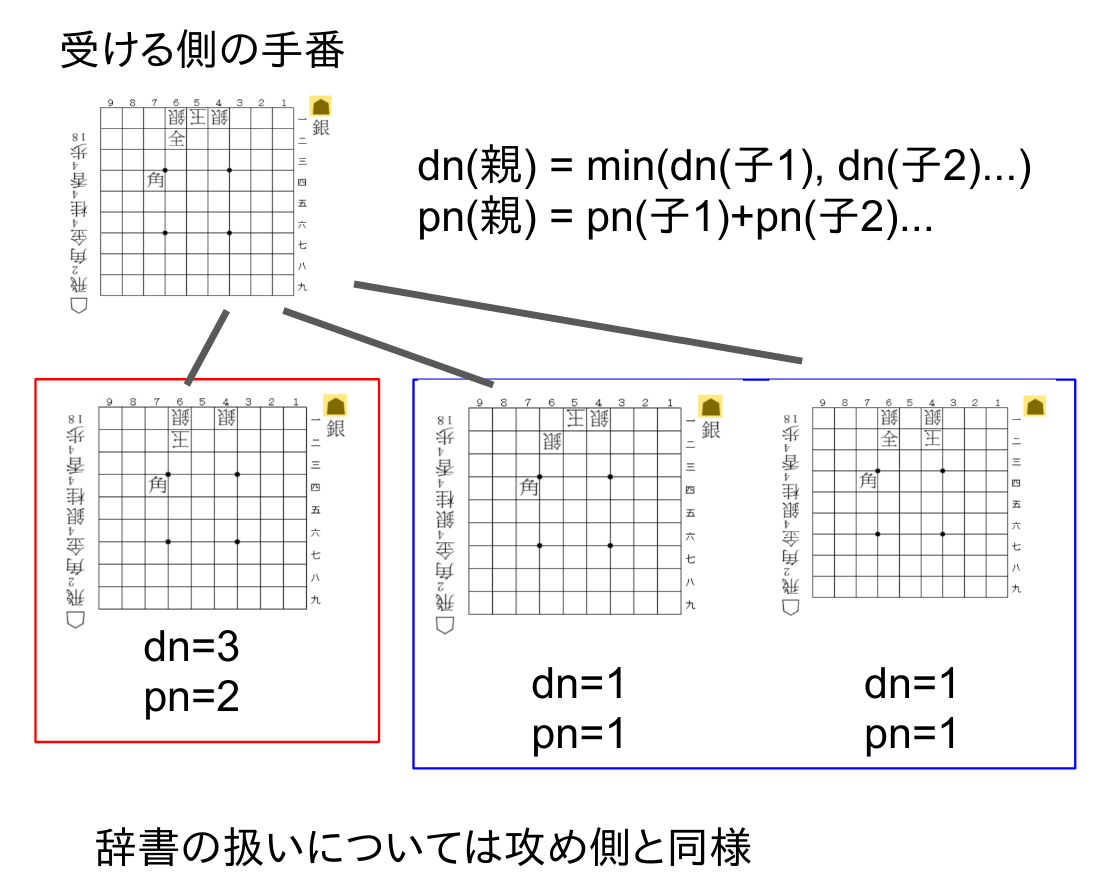
【proof numberの更新】 ある局面のproof numberはその局面(親局面)から到達できる局面(子局面)のpn、dnを用いることで更新できます。各人が最善を尽くすという仮定により、攻める側の手番では「候補手の中でどれか一つでも詰みが見つかれば詰み」、「不詰を証明するには全ての手で不詰を証明しなければならない」という条件が、受ける側の手番では「候補手の中でどれか一つでも不詰が見つかれば良い」、「詰みを証明するには全ての手で詰みを証明しなければならない」となっていることに気をつけてください。即ち、pn、dnの更新方法はどちらの手番であるかによって変わります。
辞書の扱いにも注意してください。辞書に局面が記載されていない場合、pn=dn=1で初期化された状態で辞書に局面が追加されます。
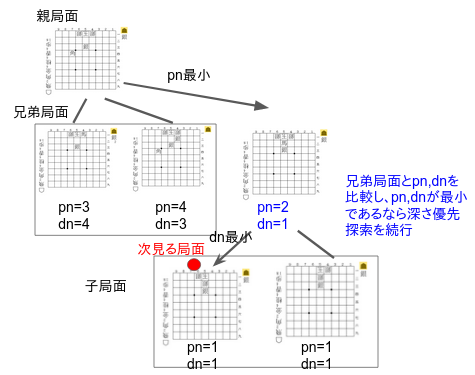
【pn、dnを使った深さ優先探索】 ハッシュテーブルを用いたdf-pn探索では各局面のpn,dnを逐次更新しながら、攻める側はできるだけ相手の受けが少ないような手(= 子局面のpnが小さいもの)を、受ける側はできるだけ次の王手が続きにくい手( = 子局面のdnが小さいもの)を優先して探索することで詰み、不詰みを高速に証明しようとしています。具体例として以下のようなpn,dnの木を使ってみましょう。現在、親局面(攻め側の手番)から最もpnが小さい局面へ探索対象が移った状態です。同じ親局面から行くことができる手を兄弟局面、今見ている局面から行くことができる局面を子局面と呼びます。
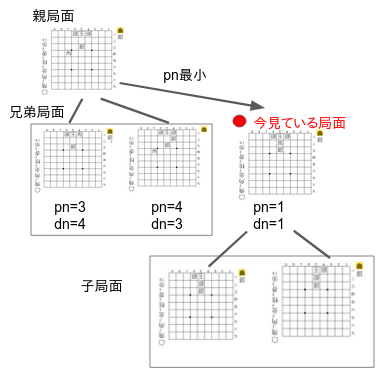
1.局面探索でまず最初に行うのは、子局面pn,dnを用いて今居る局面のpn,dnを更新することです。更新方法は上述したとおりです。
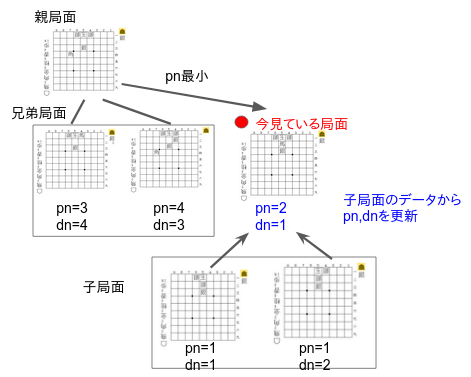
2.その後、今見ている局面のpn,dnを更新した後で、兄弟局面のpn, dnと比較を行います(より厳密にはpn, dnの2番手の値などを事前に保存しておき(付録のコード内でthpn, thdnと呼ばれている変数です)、それと比較を行います。)
3−1.このとき、今見ている局面のpn, dnが兄弟局面に比べて小さいなら、今見ている局面から最もpn、または、dn(攻め手側ならpn、受け手側ならdnを使う)が小さい子局面に探索対象を移します。
3−2.一方、pn、dnが他の兄弟局面に負けているのであれば(厳密には親局面から予測される兄弟局面のNo2との値の最大値を上回ったら)、親局面に探索対象を戻します。
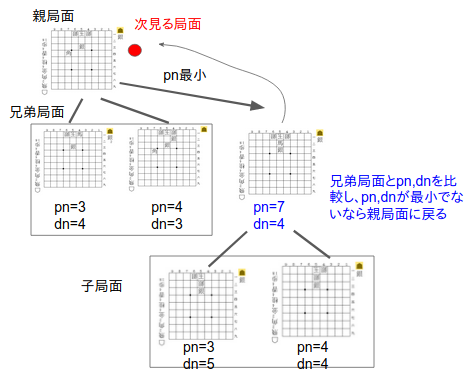
探索対象が変わったら、新しい探索対象の小局面を用いてpn, dnを更新に戻ります(1の手順)。
この探索を繰り返していくと、どこかしらの局面で詰み、または不詰み(王手の合法手がない局面)に到達します。それらの局面に到達したら、詰みの場合はpn=0、dn=∞、不詰みの局面はpn=∞、dn=0として親局面に探索対象を移します。
上記ルーチンを繰り返すことで、初期局面のpnが0になれば詰み、dnが0になれば不詰みであることを示すことが出来ます。
【inc_flagを利用した無限ループ回避】 しかし実は、上述のアルゴリズム単体は局面がループした場合に対して脆弱性があります。以下の図をみてみましょう。(原著論文の図面を改変したもの。)
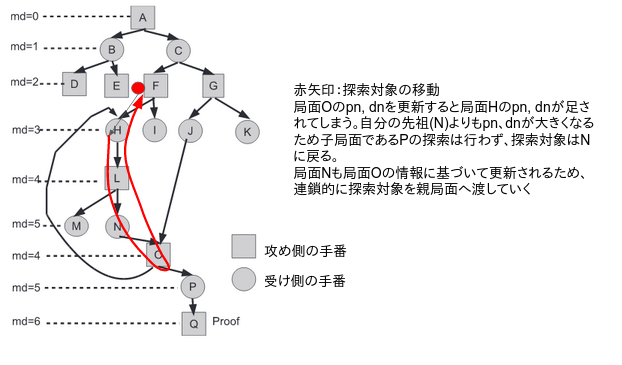
上図面のように局面のループがあると、pn/dnの更新の時点で当該局面のpn, dnは親局面のpn, dnを超えてしまいます。そのため、上述の3−2のルーチンに従い、探索局面を親局面に戻さなければなりません(2も参照)。そのため、局面P以降は探索されることがなく、局面Qが唯一の詰み筋であった場合、詰み筋を見つけることが出来ません。これを避けるためには、自分よりも先祖の局面にループした場合の特殊処理を挟む必要があります。以下の図を見てみましょう。
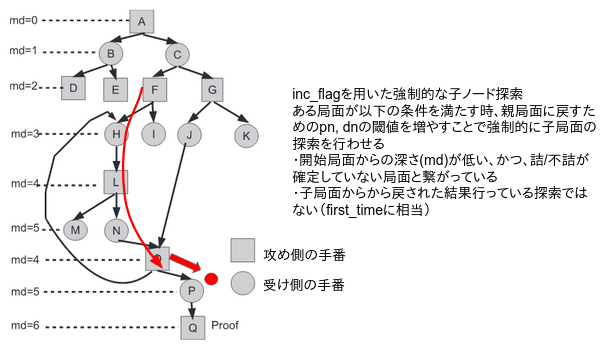
tanuki-などで採用されているアルゴリズムでは以下の条件をすべて満たす場合、局面を親に戻すためのしきい値thpn, thdnを書き換えることで、強制的に子局面を探索させるようにしています。
- 子局面に自分よりも初期局面からの距離が短い、かつ、詰み/不詰みが解っていない局面がある
- 子局面から戻された探索ではない
ループした局面のpn, dnはほかの子局面よりも大きいため、正当な子局面への探索をすることが出来ます。 上記アルゴリズムを行うことで局面の詰み/不詰みを高速に判定することが出来ます。
【df-pnで見つかる詰み筋について】 df-pnで見つかった詰み局面は最短手数であることが保証されていません。あくまでpn, dnが小さい局面から探していくため、手数が短くても変化が広い詰み筋は後回しになるからです。ちゃんと短い手数の詰み筋を見つけるにはdf-pnに手数の制限を加える必要があります。例えば、深さN以上の局面については強制的に不詰とすることで、手数をN手に縛った探索を行い、詰み筋が見つかるか否かを判別することができます(この表現、実は正しくない。詳細はオマケ参照)。
【まとめ】df-pnを使った詰将棋ルーチンについて解説をしました。本技術を用いればかなり超手数の詰将棋も見つけられるようです。
【付録】 tanuki-の詰将棋エンジンに搭載されているアルゴリズムの原著論文(英語)の疑似コードに日本語の解説を付けたもの。コードが読める人だとこっちのほうが解りやすいかも。
func DFPNwithTCA(n, thpn, thdn, inc_flag) {
// この関数が再帰的に呼ばれる。n=局面
// thpn = n のproof number(pn)がこれ以上なら探索を打ち切る
// thdn = nのdisproof number(dn)がこれ以上なら探索を打ち切る
// inc_flag thpn, thdnを増やすことで探索を強制的に打ち切らないようにする
// nが詰み、または、王手をかける手がない(不詰確定)の場合、探索を打ち切る
if (n is a terminal node) {
handle n
return;
}
first time = true; // ループに入って最初の処理かを判別
// 以下無限ループ
while (1) {
// n が探索されるのはこれが初めてならthpn, thdnの拡張は不要
if (n is a leaf) {
inc flag = false;
}
// nの子局面の中にnよりも元局面からの深さが浅い局面がある = ループしている、かつ、子局面の詰み、不詰みが確定していない
if (n has an unproven old child) {
inc flag = true; // inc_flagをon
}
// 局面nから合法手を生成、子局面のpn, dnからnのpn,dnを計算する
expand_and_compute_pn_dn(n);
if (first time && inc flag) {
thpn = max(thpn, pn(n) + 1);
thdn = max(thdn, dn(n) + 1);
}
// 局面nのpn, dnが thpn, thdnより多い
// ≒局面nの兄弟局面の中にnよりpn, dnが小さい局面がある可能性がある
if (pn(n) ≥ thpn || dn(n) ≥ thdn) break;
first time= false;
// 局面nの子局面のなかでpn, dnが最も小さいもの、2番めに小さいものを探す
n1, n2 = find_best_and_second_best_child(n);
if (n is an OR node) {
// 攻め側の場合のpn, dnの更新
thpn child = min(thpn, pn(n2) + 1);
thdn child = thdn - dn(n) + dn(n1);
else {
// 受け側の場合の更新
thpn child = thpn - pn(n) + pn(n1);
thdn child = min(thdn, dn(n2) + 1);
}
// 一番いい子ノードに対して再帰的に探索
DFPNwithTCA(n1, thpn child, thdn child, inc flag);
}
【おまけ df-pnのN手詰ルーチン】 深さN以上の局面については強制的に不詰とするというルーチンは実は愚直に実装するとクラッシュする恐れがあります。というのも、詰将棋の各々の局面に到達するために掛かる手順は一通りである保証はなく、N手以上のものから、N以下のものまで含まれうるからです。例えば、あるルートでの探索でN手以上かかって不詰と判断された局面が例えば別の詰み筋の変化の中に含まれていると「親局面も子局面も詰みが確定した不詰みの局面」が生じてしまいます。これを防ぐ簡単な方法としてはN手以上かかった、かつ、未だ探索されたことのない局面についてのみ不詰とするというものがあります。しかしこの方法も、詰将棋の各々の局面に到達するために掛かる手順は一通りではないという問題を根本的には解決できておらず、N手で詰まないということを厳密に証明することはできません。
高速な詰将棋アルゴリズムを完全に理解したい(ver3)
Qhapaq アドベント将棋記事9日目
※:連載記事ですが前回までの記事をmergeした記事になりますので過去作は読まなくても大丈夫です。
今の詰将棋アルゴリズムで最強と言われているハッシュテーブル+df-pn探索による詰将棋アルゴリズムの完全理解を目指していきます。今回はproof numberやハッシュテーブルなどの探索で用いられる単語の意味を説明します。
参考文献: memo.sugyan.com

【proof numberとは】 proof numberとは平たく言えば詰将棋専用の盤面評価値みたいなものです。通常の盤面評価値と違って、詰み証明のための評価値(pn)と不詰証明のための評価値(dn)があります。pn、dnは「この局面の詰み/不詰を証明する為に調べなければならない局面の数」であり、値が小さいほど詰み/不詰に近いという扱いになります。そして、詰み /不詰が証明された局面についてはpn、dnは0になります。局面のpn、dn(厳密には非0のpn、dn)はあくまで探索途中での予測値にすぎないことに注意してください。即ち、pn、dnは探索の途中で増えたり減ったりします。
【ハッシュテーブルとは】 雑に言えば局面毎のpn、dnを保存する辞書のようなものです。将棋などのゲームでは手順前後により重複した局面が多々でてくるため、一度探索した局面を覚えておくことで計算の効率を向上させます。
【proof numberの更新】 ある局面のproof numberはその局面(親局面)から到達できる局面(子局面)のpn、dnを用いることで更新できます。各人が最善を尽くすという仮定により、攻める側の手番では「候補手の中でどれか一つでも詰みが見つかれば詰み」、「不詰を証明するには全ての手で不詰を証明しなければならない」という条件が、受ける側の手番では「候補手の中でどれか一つでも不詰が見つかれば良い」、「詰みを証明するには全ての手で詰みを証明しなければならない」となっていることに気をつけてください。即ち、pn、dnの更新方法はどちらの手番であるかによって変わります。


辞書の扱いにも注意してください。辞書に局面が記載されていない場合、pn=dn=1で初期化された状態で辞書に局面が追加されます。ハッシュテーブルを用いたdf-pn探索では各局面のpn,dnを逐次更新しながら、攻める側はできるだけ相手の受けが少ないような手(= 子局面のpnが小さいもの)を、受ける側はできるだけ次の王手が続きにくい手( = 子局面のdnが小さいもの)を優先して探索することで詰み、不詰みを高速に証明しようとしていっます。
【pn、dnを使った深さ優先探索】 具体例として以下のようなpn,dnの木を使ってみましょう。現在、親局面(攻め側の手番)から最もpnが小さい局面へ探索対象が移った状態です。同じ親局面から行くことができる手を兄弟局面、今見ている局面から行くことができる局面を子局面と呼びます。

1.局面探索でまず最初に行うのは、子局面pn,dnを用いて今居る局面のpn,dnを更新することです。更新方法は上述したとおりです。

2.その後、今見ている局面のpn,dnを更新した後で、兄弟局面のpn, dnと比較を行います(より厳密にはpn, dnの2番手の値などを事前に保存しておき(付録のコード内でthpn, thdnと呼ばれている変数です)、それと比較を行います。)
3−1.このとき、今見ている局面のpn, dnが兄弟局面に比べて小さいなら、今見ている局面から最もpn、または、dn(攻め手側ならpn、受け手側ならdnを使う)が小さい子局面に探索対象を移します。

3−2.一方、pn、dnが他の兄弟局面に負けているのであれば、親局面に探索対象を戻します。

探索対象が変わったら、新しい探索対象の小局面を用いてpn, dnを更新に戻ります(1の手順)。
この探索を繰り返していくと、どこかしらの局面で詰み、または不詰み(王手の合法手がない局面)に到達します。それらの局面に到達したら、詰みの場合はpn=0、dn=∞、不詰みの局面はpn=∞、dn=0として親局面に探索対象を移します。
上記ルーチンを繰り返すことで、初期局面のpnが0になれば詰み、dnが0になれば不詰みであることを示すことが出来ます。
長く続いた詰将棋解説も終盤戦(あと1回か2回)。次回は無限ループの回避アルゴリズムを紹介します。
【付録】 tanuki-の詰将棋エンジンに搭載されているアルゴリズムの原著論文(英語)の疑似コードに日本語の解説を付けたもの。コードが読める人だとこっちのほうが解りやすいかも。
func DFPNwithTCA(n, thpn, thdn, inc_flag) {
// この関数が再帰的に呼ばれる。n=局面
// thpn = n のproof number(pn)がこれ以上なら探索を打ち切る
// thdn = nのdisproof number(dn)がこれ以上なら探索を打ち切る
// inc_flag thpn, thdnを増やすことで探索を強制的に打ち切らないようにする
// nが詰み、または、王手をかける手がない(不詰確定)の場合、探索を打ち切る
if (n is a terminal node) {
handle n
return;
}
first time = true; // ループに入って最初の処理かを判別
// 以下無限ループ
while (1) {
// n が探索されるのはこれが初めてならthpn, thdnの拡張は不要
if (n is a leaf) {
inc flag = false;
}
// nの子局面の中にnよりも元局面からの深さが浅い局面がある = ループしている、かつ、子局面の詰み、不詰みが確定していない
if (n has an unproven old child) {
inc flag = true; // inc_flagをon
}
// 局面nから合法手を生成、子局面のpn, dnからnのpn,dnを計算する
expand_and_compute_pn_dn(n);
if (first time && inc flag) {
thpn = max(thpn, pn(n) + 1);
thdn = max(thdn, dn(n) + 1);
}
// 局面nのpn, dnが thpn, thdnより多い
// ≒局面nの兄弟局面の中にnよりpn, dnが小さい局面がある可能性がある
if (pn(n) ≥ thpn || dn(n) ≥ thdn) break;
first time= false;
// 局面nの子局面のなかでpn, dnが最も小さいもの、2番めに小さいものを探す
n1, n2 = find_best_and_second_best_child(n);
if (n is an OR node) {
// 攻め側の場合のpn, dnの更新
thpn child = min(thpn, pn(n2) + 1);
thdn child = thdn - dn(n) + dn(n1);
else {
// 受け側の場合の更新
thpn child = thpn - pn(n) + pn(n1);
thdn child = min(thdn, dn(n2) + 1);
}
// 一番いい子ノードに対して再帰的に探索
DFPNwithTCA(n1, thpn child, thdn child, inc flag);
}
藤井聡太棋聖に勝つと手に入る新タイトルSOTAについて考えてみた
遂に藤井棋聖が爆誕しました。ブログで藤井二冠が誕生する確率は75%を超えていると主張した身としては「せやろな」感がありますが、それにしても強い。強すぎるので勝った棋士なんて相当嬉しいのではなかろうか。というわけで藤井棋聖に勝った人が得られるタイトルSOTAなるものを考えてみることにしました。
【新タイトルSOTAのルール】
コンピュータ将棋の非公式チャンピオンのルールに準拠します。即ち
・初代SOTAは藤井四段(そうか、ちょっと前は四段だったんだな)
・SOTAを持つ人に勝つとSOTAが移動する
・対局は将棋棋士のレーティングサイトに準拠する
では早速見ていきましょう。
(※:基本的に段位、タイトルは2020年6月時点のもの)
【2016〜2017年】

藤井四段が将棋界で前人未到の29連勝により初代〜29代目SOTAになります。永世SOTAのルールについては特に考えていませんでしたが、恐らく永世SOTAになったことでしょう。藤井四段のお陰で2016年のSOTAの集計は非常に楽でした。
30代目にして初の藤井聡太じゃないSOTAは佐々木勇気七段。竜王戦から叡王戦に戦いの場を移しながら、最後は野月八段が怒涛の7連勝で2017年を閉じます。
【2018年】

2018年のSOTAは非常に目まぐるしく移り変わります。5月にはほぼ1年ぶりに藤井聡太SOTAが誕生。集計に疲れた私の願いに応えるかのように6連勝をしてくれます。しかし2018年の最強SOTAは、ABEMAトーナメントでも無類の強さを見せた広瀬八段。なんと12連勝。広瀬八段は勢いそのままに、羽生竜王(当時)と竜王戦で激戦を繰り広げ、遂に27年も続いた羽生善治九段が何らかのタイトルを持っている状態に引導を渡します。
年間SOTA大賞があるかは知りませんが、あったら広瀬八段にぜひ受け取ってもらいたいです。
【2019年】

2019年のSOTAは豊島-木村ラインでの殴り合いの1年と言って良いでしょう。竜王戦の挑戦者決定戦と王位戦で10試合もの死闘を繰り広げ将棋ウォッチャーはその結果に一喜一憂したものです。特に王位戦の最終試合は会場の陣屋に木村ファンが集まった結果、陣屋史上最大の混雑を記録、王位奪取が決まったときには会場でファンが涙を流す歴史的な一日となりました。惜しくも破れた豊島前王位も竜王戦への挑戦と奪取を決めその実力を示しました。
【2020年】

2020年の歴史的、もとい、今も続いている素晴らしい事件は女流SOTAが登場したことです。西山三段は昨シーズン、14勝4敗の成績を挙げながら惜しくも四段プロデビューを逃してしまいました。しかし、その悔しさをバネに(?)活躍する姿にはただただ敬服の年を示すばかりです。
【まとめ】
藤井棋聖に勝った棋士を数珠繋ぎにすると、将棋棋士が如何に実力伯仲のギリギリの戦いをしているかがお分かりになるかと思います。実力伯仲の勝負をしている上に、良く良く考えれば将棋の勝率の期待値は5割なのだから、SOTAの集計をしようものなら指が痛くなることなど目に見えていたはずなのに指を酷使したことを少々後悔しながらも、本稿が将棋を楽しむちょっとしたスパイスになってくれればと願っております。