js26歩の評価関数を公開します and 課金評価関数事業の進捗報告
2022年11月の第3回世界将棋AI電竜戦本戦、及び、 第1回マイナビニュース杯電竜戦ハードウェア統一戦に参加したJust Stop 26歩の評価関数です。定跡無しで飛車を振る、水匠をはじめとした入賞ソフトの多くに振り飛車で倒す、いずれの大会も振り飛車ソフトとしては最高成績を上げる(6位、9位)と2023年2月時点でおそらく最強の振り飛車将棋ソフトであると思われます。ふかうら王(dlshogi)向けの評価関数(model.onnx)とやねうら王に搭載できるNNUE型の評価関数(nn.bin)からなります。ただしnn.binはsqmz関数と同じ中身となっております。
ダウンロードはこちらから
深層学習モデルで特定の戦型を指すことを特徴とした評価関数については勝率測定が難しく(互角局面を使うと無意味なものになってしまうが、さりとて平手でやると同じ棋譜ばかりが作られる)強さについてはなんともフワフワした表現になってしまっていますが、大会実績を鑑みるにおそらく強いと思います。お楽しみいただければ幸いです。
【課金評価関数について。配布する際のライセンス案を考えました】
大航海時代に冒険者が貴族たちに出資を受けて航路を探したのと同じく、皆様から課金を募って評価関数を作りそれを公開するという事業を始めようとしています。
一部の人間に有償で評価関数を売却する仕様上、利用方法にいくつかのルールをつける必要があると考えています、例えば、追加学習したモデルを将棋大会で使ってもいいけど、ほぼ何も学習していないようなモデルを自作モデルとして公開されても困ると言った具合です。
将棋AI開発者や利用者のモチベーションを高めることと、課金してくれたユーザの期待を裏切らないことのバランスを取るために「販売してから一定期間については追加学習をしたモデルの公開を禁止する。一定期間経過後についてはCC-BY-SAライセンスとする」というライセンスをつけることを考えています。
以下にライセンスの文面案を記載します。ご意見アドバイスありましたらお願いします
======以下文面案======
【個人利用向けライセンス】
本学習済評価関数(model.onnx, model.pth)を対局・定跡作成・各種将棋AIの大会にご利用いただけます。ただし、各種ドキュメントファイルやPR文章に本学習済評価関数を使ったことを明記してください。また、本学習済評価関数を追加学習して得られた評価関数についてはその公開を禁止します。
【デュアル・ライセンス】
Qhapaq開発チームは、本学習済評価関数を、将棋AI開発の促進と各種将棋AIの大会の競技性の維持の両立を目的とし、A年X月Y日以降は上記個人利用向けライセンスと、下記開発者向けライセンスによるデュアル・ライセンスモデルで提供します。
【開発者向けライセンス(A年X月Y日より有効)】
A年X月Y日以降については本学習済評価関数をCC-BY-SA3.0のもとご利用いただけます。詳細は
https://creativecommons.org/licenses/by-sa/3.0/deed.ja
をご参照ください
======文面案終わり======
最初の販売用の評価関数の学習はまもなく終わる見込みです(自前PCで回してるから遅い遅い)。販売する以上、「買ったけど使えなかったよ」というケースを減らすためにドキュメントやexampleを書く作業を頑張っています(これが案外大変)。使い方わからなかった人はnote経由で返金申請してという運用にしたいと思っていますがnoteの返金期限が24時間なのでできるだけ事前に丁寧な説明を心がけたいところ。
Bitsjourney : AI that transforms images into 1980s video games
Do you ever feel nostalgia for image quality? Nowadays 4K images became quite common, and even the images are now drawn by AI instead of humans. However not a few of you may miss the days when you had to spark from an electrical outlet to display Pikachu on a screen with only 256 pixels.
In response to your desires (?), I have released "Bitsjourney", an engine that converts high quality images to look like 1980s games. This application make you a dot painter of the end of the century.
【Examples】

NES-ish images

Looks like a 1990's gal game.

AI-generated images are of course supported (original images are generated bythis waifu does not exist)
【Bitsjourney is open source!】
Source code is available from here.
You can run core algorithms of Bitsjourney from Python and nodejs.
WIP : The UI of the chrome extension should be more improved. However, it was too difficult for me. Your advice and contribution is demanding.
FAQ: Can we call this AI? Isn't it just an algorithm?
A: I think it was called AI around the end of the 20th century. I think that in about 50 years from now, the various things that are called AI today will not be called AI, but just neural nets.
【License】
-
© Kizuna AI, SCP Foundation., CC BY-SA 3.0
-
Joichi Ito - Original text: Taken by author Transferred from English Wikipedia
画像を1980年代のゲームっぽく変換するAI「Bitsjourney」を公開しました
唐突ですが、皆様は画質に対するノスタルジーを感じることはないでしょうか。4K画質は当たり前、その画像さえも人間ではなくAIが描くようになった時代ですが、256ピクセルしかない画面にピカチュウを表示するためにコンセントから火花を散らしていた時代が懐かしくなる人も少なからずいることでしょう。
そんな皆様の声を受けて(?)高画質の画像を1980年代のゲームっぽく変換するエンジン「Bitsjourney」を作ってみました。これさえあればあなたも世紀末のドット絵師です。
【使い方】
例えばこんな感じの画像が生成されます。

ファミコンっぽい
1990年代のスーパーファミコン画質も生成できます。

1990年代のギャルゲーっぽい

AIが作った画像にももちろん対応(元画像はthis waifu does not existで生成)
【Bitsjourneyはオープンソースです】
ソースコードはこちらから取得できます。
pythonやnodejsからの利用も可能ですので画像フォルダのデータを一括変換などをしたいエンジニアの方はこちらをご利用ください。
chrome extensionのUIはjavascriptが難しすぎて妥協したところが多々ありますので詳しい人のPRを切に募集しております。
ちなみに画像圧縮にはIMAKITAでも使われた独自のアルゴリズムが実装されています。k-meansとほぼ同じ画質を維持しながら、k-meansに比べてオーダー違いに早いです(256色でも数秒程度で計算ができる。k-meansだと画像サイズによっては数分かかる)
FAQ:これをAIと言って良いの? AIと言うよりアルゴリズムじゃないかな?
A:20世紀末ぐらいにはAIと呼ばれていたと思います。今AIって呼ばれてる諸々も50年後ぐらいにはAIじゃなくてただのニューラルネットっていわれるんじゃないですかね。
【ライセンス情報】
-
© Kizuna AI, SCP Foundation., CC BY-SA 3.0
-
Joichi Ito - Original text: Taken by author Transferred from English Wikipedia
2022年1月時点で最強(多分)の飛車を振る評価関数を公開します
昨日の順位戦で嬉しいことがあったので評価関数を公開します。水匠5に対してQPDの教師データによる追加学習を施したものです(ので、この関数が強いのはほぼたややん氏のおかげです)
ダウンロードはこちらから
関数名はSuisho-Qhapaq-MixtureZ関数です。略してスク水(SQMZ)関数とでもお呼びください。飛車を振る確率が高い関数(pearl)と、レーティングを高くするために振り飛車率を下げた関数(dia)とがあります。
【強さ、振り飛車率】
最新のレーティングはこちらから。
pearlバージョンは30%程度の確率で飛車を振ってくれます。QPDとほぼ同等の強さ+振り飛車率が向上(20%→30%)ので実質的に強くなったと言えると思われます。diaバージョンは水匠5とほぼ同程度のレーティングでありながら5%〜10%程度の確率で飛車を振ってくれます。持ち時間が長いと居飛車率が上がるようですが......
【補足トリビア】
やねうら王7の評価関数としてお使いください。FV_SCALEを24にすることも忘れないでおいてください。
QPD vs 水匠4のときよろしく、vs振り飛車性能の高さからdiaバージョンは水匠5よりも高いレーティングが出ていますが誤差の範囲だと思います。ちなみに中の人は自分が出した関数が微妙な差でsotaになると気まずいので早く負けてくれと思ってます。
【振り飛車の一例】
「居飛車をやろうとおもったけど、中飛車にしたうえで26の歩は銀冠に使うよ」みたいな主体性のない振り飛車を指します

Qhapaq Pretty Daabiの評価関数と教師データを公開します
第2回世界将棋AI電竜戦お疲れ様でした。Qhapaqチームは本大会に「Qhapaq Pretty Daabi(チーム名:トレセン学園将棋部)として参加し、大会総合成績15位+振り飛車最強賞+独創賞をとることができました。
参加、視聴、寄付、運営など本大会を支えてくれた全ての方々への感謝の気持を込めてQPDの評価関数を公開いたします。
【評価関数のダウンロードはこちらから】
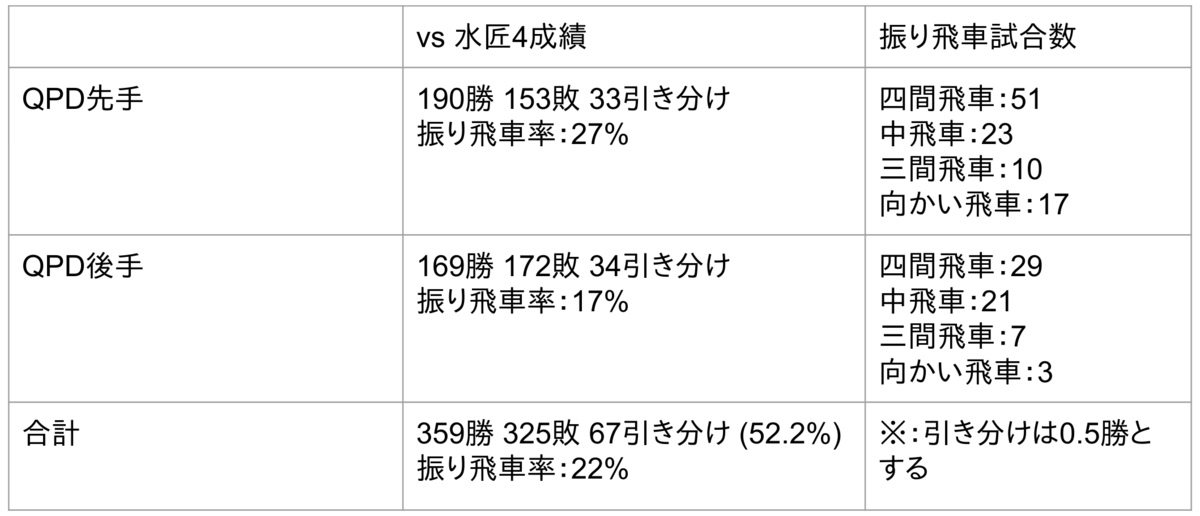
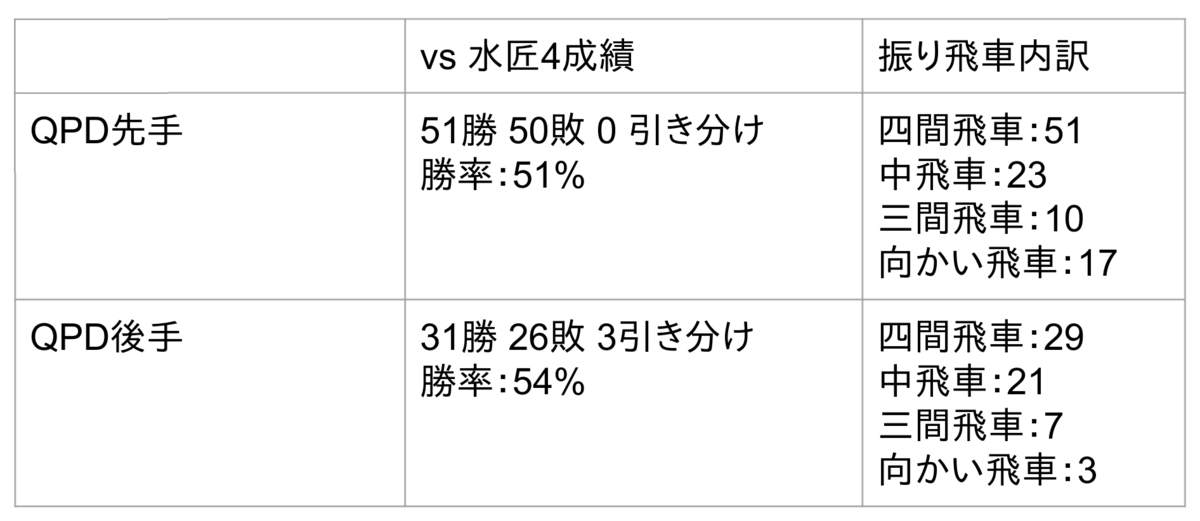
今回の評価関数はオールラウンダー型です。状況に応じて居飛車と振り飛車を使い分ける設計になっています。 やねうら王6.3による vs 水匠4での勝率、及び、振り飛車率(飛車を28から58/68/78/88に動かした棋譜の割合なのでガチの振り飛車じゃないのも含まれてるかも)は以下のとおりです。

各ソフトとの対局結果はQhapaqのHPからもご参照いただけます。一瞬とはいえ(?)SOTAを更新しました。なお、QPDの評価関数名がfuri1016になっていますが、これは開発上の都合によるものです(QPDの誕生日は10月16日だったという話ですな......)
【QPDの教師データ(ステマ配合の元)】
今回はさらにQPDの学習に用いた教師データと学習ログも共有します。皆で飛車を振りましょう。なお、本データには利用規約があることにご注意ください。利用規約は凄く雑に言えば、「これを使って学習した評価関数を大会に出したり公開する場合はデータを使った旨を書いてくださいね」というものです。QPDのデータがどのように使われたかを開発者が知りたいから用意したものです。皆様の自由な創作を妨げるためのものではないので、困った場合は開発者にご相談いただければ、できるだけご希望に添えるようにいたします。
【教師データのダウンロードはこちらから】
本大会ではディープ勢に対して振り飛車で一度も勝つことが出来ませんでしたが、皆の力を合わせれば次こそ振り飛車でディープ勢をボコることができるでしょう。
今後共、Qhapaqチームとコンピュータ将棋をよろしくお願い申し上げます。
棋力ゼロでも棋戦解説はできるのか(実践編)
第二回電竜戦にQhapaq Pretty Daabiで参加しました。前回の大会で3位入賞+最強振り飛車ソフトの称号をゲットしたことに味をしめ、今年も振り飛車ソフトで参加しましたが想像以上にボコボコにされて予選落ちをしてしまいました。
さて、振り飛車が負けたときに備えて本大会では将棋ソフト開発以外の事業にも手を出してみようということで、将棋解説用のGUIエンジンを作ってみました。
将棋の手の意味を理解する上で主に用いられる情報は「その手の代わりにパスを指したらどのような変化になるか(≒相手の狙いは何か)」や、「その後の手の進行においてその手の有無で評価値がどの程度変わるか」です(詳しくはPR文章にも記載)。
これらの情報をユーザがリアルタイムで得られるようにすれば棋力ゼロの開発者でも将棋実況解説ができるのではないでしょうか、やってみた結果がこちらです。

これは第2回電竜戦【予選リーグ】 2回戦☗Qhapaq Pretty Daabi-☖二番絞り(ビール工房HFT支店)の終盤で出てきた局面の解析結果です。後手の二番絞りは上の局面で94歩と端歩をついてきましたが、その意味がイマイチわかりません。先手が8筋から攻撃を仕掛けてくる中でなぜ端歩なのでしょうか。
それを明らかにするために、94歩の代わりにパスを選んだ場合の変化をみてみましょう。

ここからさらに変化を見ていくと、71飛、83歩成、同歩、同飛成と進んでいきます。仮にここで94歩入っていたらどうなるでしょう。

94歩が入っていると飛車の逃げ道が増えているのがわかります。そして、先程の変化に比べ93に飛車を逃がす変化は評価値的に見ても470ぐらい得(先手+180→後手+290)しているのがわかります。94歩は飛車の逃げ道を増やすための手だったのです。
実戦の変化では94歩が指された結果、65桂打の変化が先手にとって望ましくなくなったため、先手は別の手(65桂馬の代わりに84飛車)を指したため、94歩の意味は棋譜を眺めるだけでは理解するのが難しくなっていました。
しかし、様々な手順をインタラクティブに表示することで棋力が少ないプレイヤーでも手の意味を理解しやすくなっているのがわかります。
【ニコニコ生放送をやってみた】
このツールを引っさげてニコニコ生放送で中継、及び反省会をやってみました。改めて見ると私が非常にテンパっているのがわかります。また、電竜戦でのソフトの指しては非常に早く入力が基本的に間に合わないため放送としてはグダグダの結果になってしまいました。将棋系vtuberやyoutuberは改めて凄いと思いました。ただ、実況が上手く行かなかったのはツールの不備というよりは私の実力不足だと思うので今後とももう少しずつクオリティーを上げていきたいところです
↓ ディープ系ソフトに殴られてふてくされた中の人による黒歴史解説動画。基本的に私がテンパってる以外見どころがないのですが、orqhaにはおせわになりました、QQRも使ってましたなどのコメントいただけたのは本当に嬉しかったです。ありがとうございました。腹筋は割れてないです
大会は予選落ちしましたがそのおかげで明日は気楽に中継ができると思われます。リアルタイム解説は辛いので昼食休憩時に振り返り解説などになると思われますがお付き合いいただけると幸いです。結局2日目も勝ちたくなったり鯖が不安定だったりで全対局終わるまで中継できませんでした。申し訳ないです。あと2日目も見に来てくれた人、ありがとうございました!!
【おまけ】
今回のQPDの評価関数の強さ。オールラウンダー型の評価関数で定跡抜きでは2割程度の確率で飛車を振った上で水匠4に勝ち越すというかなり強い関数を用意できたのですが、大会では全然結果が出ませんでした。他ソフトがもっと強かったのか、長時間で弱かったのか、ディープとの相性の問題か、振り飛車が悪いのか......
第31回世界コンピュータ将棋選手権で変態将棋を指してみた件
第31回世界コンピュータ将棋選手権に参加された皆様、視聴してくださった皆様、誠にありがとうございます。QhapaqチームはMolQha-として参加して予選12位で敗退となりました。敗退して隠すこともなくなったので、大会を通じて色々考えたことを紹介していきたいと思います。
【新しいことに色々挑戦してみた】
電竜戦で振り飛車をコンセプトにして勝ったのに味をしめて(そして山崎A級の爆誕を祝って)本大会コンセプトは「変な将棋を指す」というものにしました。せっかくだから色々新しいものを作ってみようとyoutubeにチャンネルを立てたりもしてみました。
【変態将棋、全然勝てない】
解説動画でも簡単に述べていますが将棋AIの戦型を狙った形で分散させるのは簡単ではありません。手で定跡を作ろうとすると恐ろしい数の局面を入れなければならなくなりますし、かといって「後手の最初の2手は必ず34歩、44歩とする(四間飛車の典型ムーブ)」みたいな作りにすると、先手が「76歩、22角成(一手損、角交換四間飛車)」としてきたときに死んでしまいます。
こうした問題を解決するためにMolQha-の開発時間の大半は特定の戦型の少数の棋譜からその戦型を指しこなせるシステムの設計に費やしました。
そうした努力の甲斐あって、ある程度自動的に特定の戦型を研究できるシステムが完成。これで嬉野流や一間飛車を試しまくるぜヒャッハーと思った矢先。
これらの戦型が今の将棋AIだと全く勝てないことが判明します。どのぐらい勝てないかというと後手で勝率が3割を切る程度に勝てないことが発覚しました。
【変態将棋の何がいけないのか】
ここでは後手番の話に絞ります。というのも大会では試合の半数ぐらいは後手番になるわけですし、良い後手番の戦略が見つかれば先手番でも同じことができると期待できるからです。
様々な戦型を試した結果、後手番の勝率は初手34歩、84歩、32金以外の手を選ぶと激減(例えば初手42銀とか)することがわかりました。この3手以外の手を指してしまうと、先手番だけが一方的に飛車先の歩を交換することが出来てしまう(14歩? 知らない子ですね)からです。
それならいっそ嘘矢倉でもやったろうかと思いましたが、先手の角道が自由なまま後手の角道を閉じてしまうのも駄目なようです。なら振り飛車じゃとも思いましたが、振り飛車は水匠系列はともかく、たぬき、illqha系列に対しては異常に勝率が悪い(これも勝率3割弱)ことがわかりました。
そして色々試した結果として見つかった一番マシな戦略が初手94歩でした。初手94歩は先手番だけが一方的に飛車先の歩を交換することを可能とする手ではありますが、72銀や62銀に比べると勝率が5%ちょっと高い(後手番勝率は35%程度になる)ことがわかったのです。
これを元に先手の戦略も決めます。先手の初手16歩はWCSC29で妖怪惑星Qhapaqが使った技ではありますが、初手16歩だけだと角換わりの局面に一致してしまう可能性があります。変態将棋をやるためには2手パスを行うことで後手側に一方的に飛車先の歩を交換する権利を与えねばなりません。
というわけで、先手番では端歩を突き越してもらうことにしました。不思議なことにも、先手の歩の突き越しはNNUEミラーに於いては勝率が悪くない(55%前後)こともわかりました。
斯くしてMolQha-のコンセプトは「飛車先の歩交換よりも端の位」というものになりました。評価関数は様々な変態系で高い勝率を誇った電竜戦-tsecのtanuki-をベースに、後手番での勝率が高くなるような追加学習を施したものを使いました(まさか、コレがフラグになるとは
【ディープ、いうほど強いか?】
本大会の最大の注目株は深層学習(ディープラーニング)を使った将棋エンジンでした。なにせご家庭用のGPUでスリッパを使った既存エンジンを倒していたわけですから、本番の計算リソースではレート5000すら超える(今までの最強はせいぜい4500ぐらい)とさえ言われていました。
しかし、私はコレに懐疑的でした(電竜戦でgct、dlshogiと同盟を組みながら、美味しいところを持って行かれたことを根に持ってるという説もある)。というのも、floodgateで時々流れてくるgct+v100やらgct+a100がちょくちょく負けていたからです。
勿論、どんな強いソフトでも負ける可能性はあります。ただ、(AlphaZeroの論文などで描かれてるグラフなどから)補外されたa100利用時のレートに比べると統計的に無視できないレベルで負けていました。
R5000は出ない方に私は賭けていますが、果たしてそれが検証できるほどfgに駐在してくれるのか......(ドキドキ https://t.co/EoB1laKNAp
— Ryoto_Sawada🌗Qhapaq (@Qhapaq_49) 2021年4月19日
a100スーパーマシンgctがテスト終了したようですな。本番でどれだけ強くなるかはまだ未知数ですが、レート5000はないやろという読みについてはおじさんの勝ちでいいかな?
— Ryoto_Sawada🌗Qhapaq (@Qhapaq_49) 2021年4月20日
ディープ系列が長時間で強くならない理由として2つの理由を考えていました。ひとつは、探索過程で読んだ手をすべて覚えておかなければならない関係で深く読める量に限界があるということ。もう一つは、長い手数の良くない変化が見つかったときに従来エンジンはすぐに最善手を切り替えるのに対して、複数回ランダムプレイを行うことによる合議(に近いルール)で指し手を決めるディープ系列では長時間探索すればするほど、新しい手を受け入れにくくなることです(この問題は探索パラメタを弄ることで軽減はできるのだが)。
この予想は大会で大当たりとなるのですが、gct, dlshogiチームを始め多くの人が凄い時間と努力を積み重ねてディープ系列のエンジンを作っていることも知っていたのでなんとも気まずい感じになってしまいました。
【MolQha-自体の大会の雑な振り返り】
全体の成績は以下のようになりました(以下敬称略)
1.いちびん(先手、勝ち)
2.習甦(後手、勝ち)
3.二番絞り(先手、負け)
4.sakura(後手、勝ち)
5.Qugiy (先手、負け)
6.HoneyWaffle(後手、勝ち)
7.PAL(先手、負け)
8.koron(後手、引き分け)
9.elmo(後手、引き分け)
電王トーナメントでさんざん後手番ばかり引かされたことをネタにし続けた結果、すっかり先手番で勝てない体になってしまいました。また、本大会ではあるまじきミスをしてしまいました。それは負けたら予選突破が厳しくなる8,9試合目で千日手にならないようにする設定をミスった(8試合目は完全に忘れてた、9試合目はなんか設定をミスったっぽい)ことです。
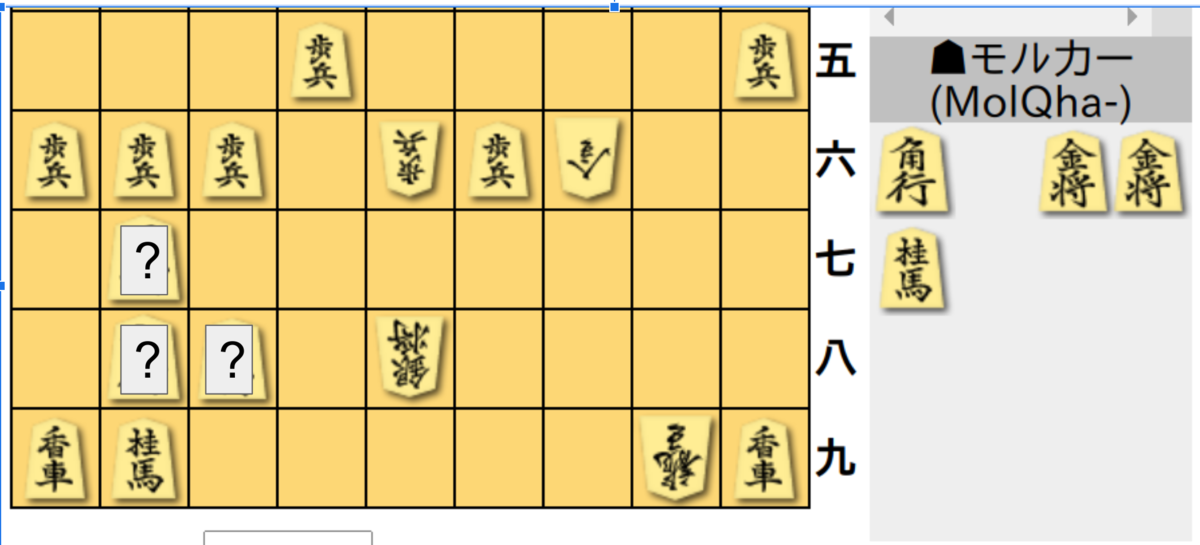
クイズ:「?」に入る駒は何でしょう
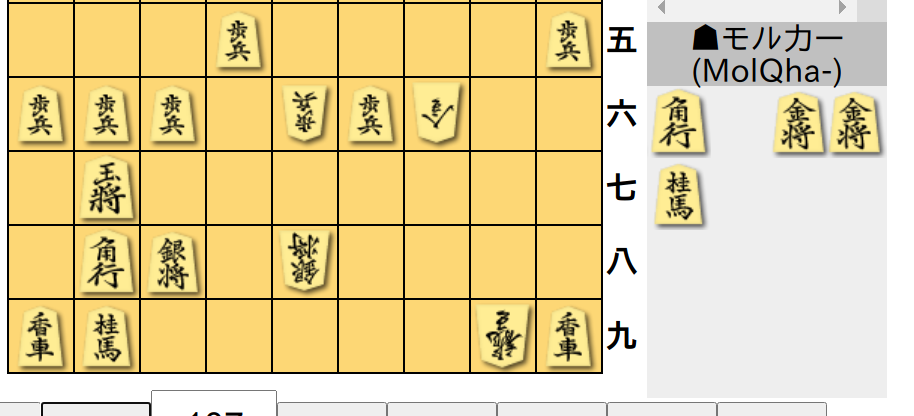
答え:銀冠ではない
斯くしてMolQha-の挑戦は終わってしまいました。ただ唯一良かったこととして、変な将棋はいっぱいさせたと思います。今後共、コンピュータ将棋をよろしくお願い申し上げます。