高速な詰将棋アルゴリズムを完全に理解したい(完成版)
Qhapaq アドベント将棋記事10日目
今の詰将棋アルゴリズムで最強と言われているハッシュテーブル+df-pn探索(depth first - proof number)による詰将棋アルゴリズムの完全理解を目指していきます。
参考文献: memo.sugyan.com
【proof numberとは】 proof numberとは平たく言えば詰将棋専用の盤面評価値みたいなものです。通常の盤面評価値と違って、詰み証明のための評価値(pn)と不詰証明のための評価値(dn)があります。pn、dnは「この局面の詰み(proof number)/不詰(disproof number)を証明する為に調べなければならない局面の数」であり、値が小さいほど詰み/不詰に近いという扱いになります。そして、詰み /不詰が証明された局面についてはpn、dnは0になります。局面のpn、dn(厳密には非0のpn、dn)はあくまで探索途中での予測値にすぎないことに注意してください。即ち、pn、dnは探索の途中で増えたり減ったりします。
【ハッシュテーブルとは】 雑に言えば局面毎のpn、dnを保存する辞書のようなものです。将棋などのゲームでは手順前後により重複した局面が多々でてくるため、一度探索した局面を覚えておくことで計算の効率を向上させます。
【proof numberの更新】 ある局面のproof numberはその局面(親局面)から到達できる局面(子局面)のpn、dnを用いることで更新できます。各人が最善を尽くすという仮定により、攻める側の手番では「候補手の中でどれか一つでも詰みが見つかれば詰み」、「不詰を証明するには全ての手で不詰を証明しなければならない」という条件が、受ける側の手番では「候補手の中でどれか一つでも不詰が見つかれば良い」、「詰みを証明するには全ての手で詰みを証明しなければならない」となっていることに気をつけてください。即ち、pn、dnの更新方法はどちらの手番であるかによって変わります。
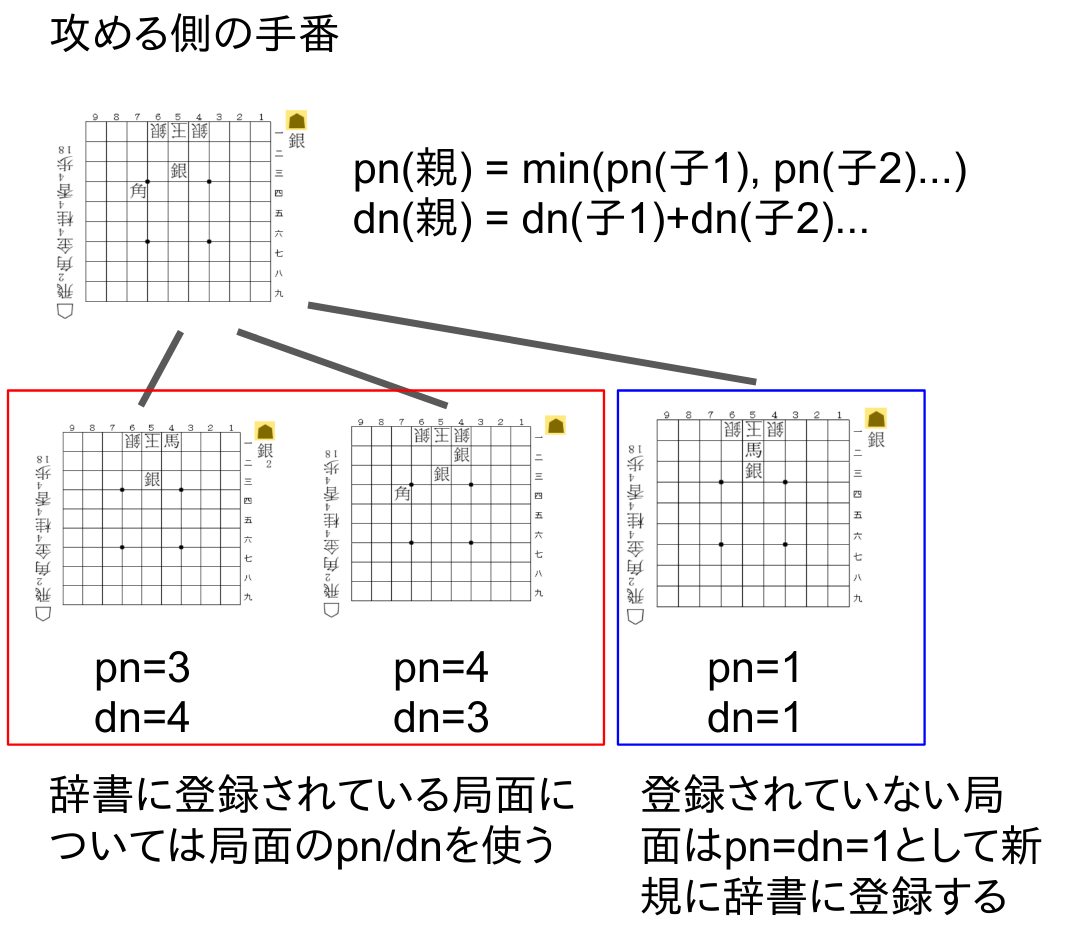
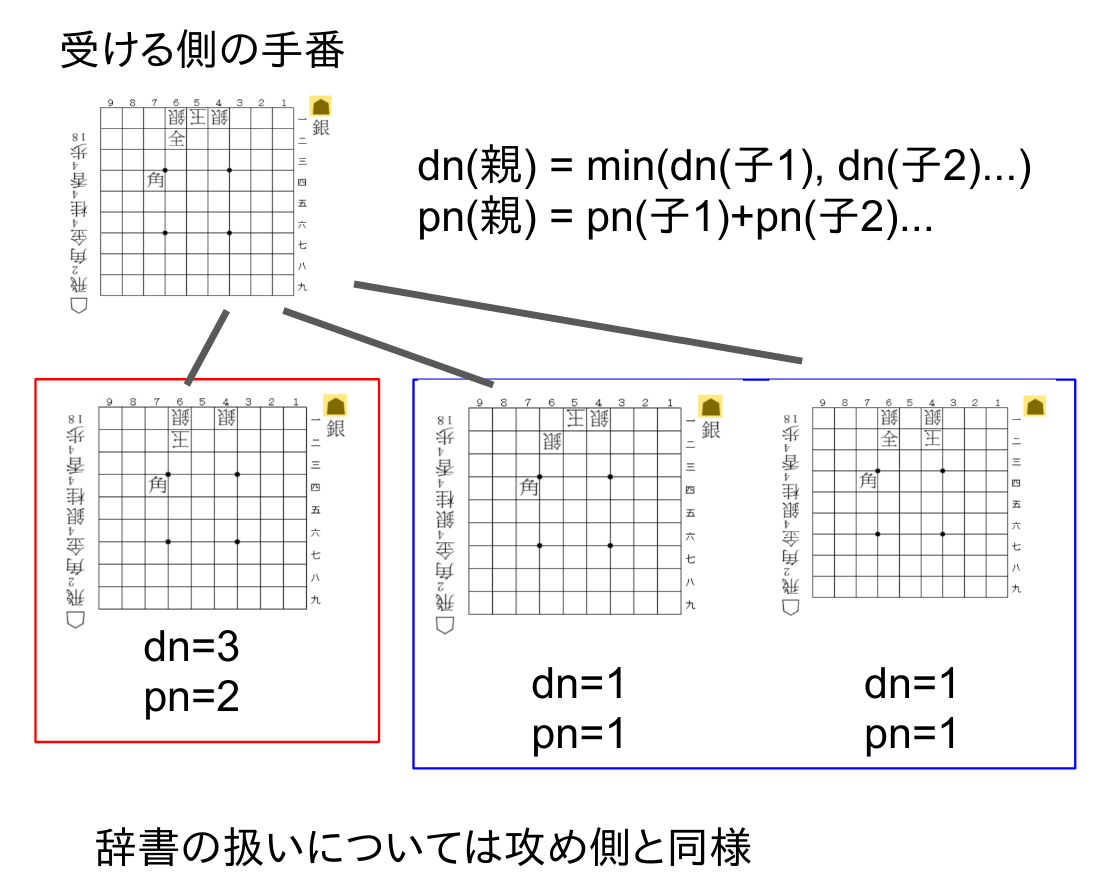
辞書の扱いにも注意してください。辞書に局面が記載されていない場合、pn=dn=1で初期化された状態で辞書に局面が追加されます。
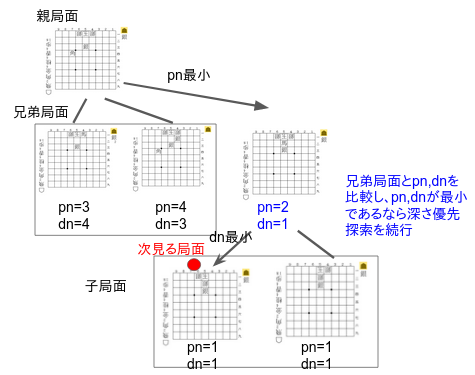
【pn、dnを使った深さ優先探索】 ハッシュテーブルを用いたdf-pn探索では各局面のpn,dnを逐次更新しながら、攻める側はできるだけ相手の受けが少ないような手(= 子局面のpnが小さいもの)を、受ける側はできるだけ次の王手が続きにくい手( = 子局面のdnが小さいもの)を優先して探索することで詰み、不詰みを高速に証明しようとしています。具体例として以下のようなpn,dnの木を使ってみましょう。現在、親局面(攻め側の手番)から最もpnが小さい局面へ探索対象が移った状態です。同じ親局面から行くことができる手を兄弟局面、今見ている局面から行くことができる局面を子局面と呼びます。
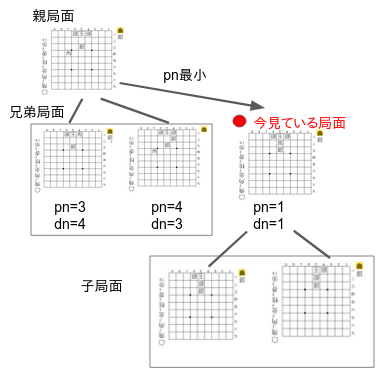
1.局面探索でまず最初に行うのは、子局面pn,dnを用いて今居る局面のpn,dnを更新することです。更新方法は上述したとおりです。
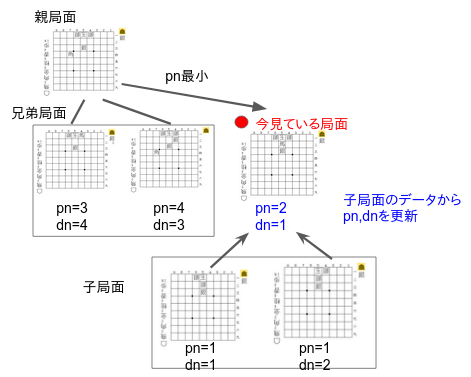
2.その後、今見ている局面のpn,dnを更新した後で、兄弟局面のpn, dnと比較を行います(より厳密にはpn, dnの2番手の値などを事前に保存しておき(付録のコード内でthpn, thdnと呼ばれている変数です)、それと比較を行います。)
3−1.このとき、今見ている局面のpn, dnが兄弟局面に比べて小さいなら、今見ている局面から最もpn、または、dn(攻め手側ならpn、受け手側ならdnを使う)が小さい子局面に探索対象を移します。
3−2.一方、pn、dnが他の兄弟局面に負けているのであれば(厳密には親局面から予測される兄弟局面のNo2との値の最大値を上回ったら)、親局面に探索対象を戻します。
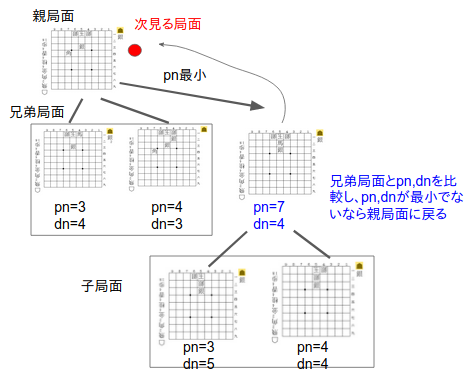
探索対象が変わったら、新しい探索対象の小局面を用いてpn, dnを更新に戻ります(1の手順)。
この探索を繰り返していくと、どこかしらの局面で詰み、または不詰み(王手の合法手がない局面)に到達します。それらの局面に到達したら、詰みの場合はpn=0、dn=∞、不詰みの局面はpn=∞、dn=0として親局面に探索対象を移します。
上記ルーチンを繰り返すことで、初期局面のpnが0になれば詰み、dnが0になれば不詰みであることを示すことが出来ます。
【inc_flagを利用した無限ループ回避】 しかし実は、上述のアルゴリズム単体は局面がループした場合に対して脆弱性があります。以下の図をみてみましょう。(原著論文の図面を改変したもの。)
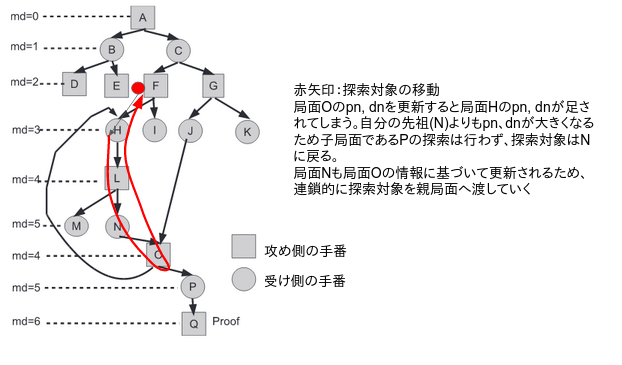
上図面のように局面のループがあると、pn/dnの更新の時点で当該局面のpn, dnは親局面のpn, dnを超えてしまいます。そのため、上述の3−2のルーチンに従い、探索局面を親局面に戻さなければなりません(2も参照)。そのため、局面P以降は探索されることがなく、局面Qが唯一の詰み筋であった場合、詰み筋を見つけることが出来ません。これを避けるためには、自分よりも先祖の局面にループした場合の特殊処理を挟む必要があります。以下の図を見てみましょう。
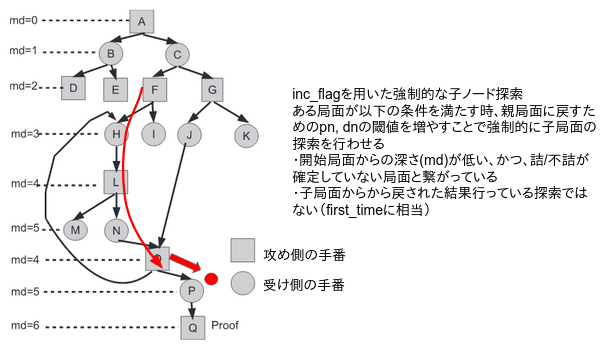
tanuki-などで採用されているアルゴリズムでは以下の条件をすべて満たす場合、局面を親に戻すためのしきい値thpn, thdnを書き換えることで、強制的に子局面を探索させるようにしています。
- 子局面に自分よりも初期局面からの距離が短い、かつ、詰み/不詰みが解っていない局面がある
- 子局面から戻された探索ではない
ループした局面のpn, dnはほかの子局面よりも大きいため、正当な子局面への探索をすることが出来ます。 上記アルゴリズムを行うことで局面の詰み/不詰みを高速に判定することが出来ます。
【df-pnで見つかる詰み筋について】 df-pnで見つかった詰み局面は最短手数であることが保証されていません。あくまでpn, dnが小さい局面から探していくため、手数が短くても変化が広い詰み筋は後回しになるからです。ちゃんと短い手数の詰み筋を見つけるにはdf-pnに手数の制限を加える必要があります。例えば、深さN以上の局面については強制的に不詰とすることで、手数をN手に縛った探索を行い、詰み筋が見つかるか否かを判別することができます(この表現、実は正しくない。詳細はオマケ参照)。
【まとめ】df-pnを使った詰将棋ルーチンについて解説をしました。本技術を用いればかなり超手数の詰将棋も見つけられるようです。
【付録】 tanuki-の詰将棋エンジンに搭載されているアルゴリズムの原著論文(英語)の疑似コードに日本語の解説を付けたもの。コードが読める人だとこっちのほうが解りやすいかも。
func DFPNwithTCA(n, thpn, thdn, inc_flag) {
// この関数が再帰的に呼ばれる。n=局面
// thpn = n のproof number(pn)がこれ以上なら探索を打ち切る
// thdn = nのdisproof number(dn)がこれ以上なら探索を打ち切る
// inc_flag thpn, thdnを増やすことで探索を強制的に打ち切らないようにする
// nが詰み、または、王手をかける手がない(不詰確定)の場合、探索を打ち切る
if (n is a terminal node) {
handle n
return;
}
first time = true; // ループに入って最初の処理かを判別
// 以下無限ループ
while (1) {
// n が探索されるのはこれが初めてならthpn, thdnの拡張は不要
if (n is a leaf) {
inc flag = false;
}
// nの子局面の中にnよりも元局面からの深さが浅い局面がある = ループしている、かつ、子局面の詰み、不詰みが確定していない
if (n has an unproven old child) {
inc flag = true; // inc_flagをon
}
// 局面nから合法手を生成、子局面のpn, dnからnのpn,dnを計算する
expand_and_compute_pn_dn(n);
if (first time && inc flag) {
thpn = max(thpn, pn(n) + 1);
thdn = max(thdn, dn(n) + 1);
}
// 局面nのpn, dnが thpn, thdnより多い
// ≒局面nの兄弟局面の中にnよりpn, dnが小さい局面がある可能性がある
if (pn(n) ≥ thpn || dn(n) ≥ thdn) break;
first time= false;
// 局面nの子局面のなかでpn, dnが最も小さいもの、2番めに小さいものを探す
n1, n2 = find_best_and_second_best_child(n);
if (n is an OR node) {
// 攻め側の場合のpn, dnの更新
thpn child = min(thpn, pn(n2) + 1);
thdn child = thdn - dn(n) + dn(n1);
else {
// 受け側の場合の更新
thpn child = thpn - pn(n) + pn(n1);
thdn child = min(thdn, dn(n2) + 1);
}
// 一番いい子ノードに対して再帰的に探索
DFPNwithTCA(n1, thpn child, thdn child, inc flag);
}
【おまけ df-pnのN手詰ルーチン】 深さN以上の局面については強制的に不詰とするというルーチンは実は愚直に実装するとクラッシュする恐れがあります。というのも、詰将棋の各々の局面に到達するために掛かる手順は一通りである保証はなく、N手以上のものから、N以下のものまで含まれうるからです。例えば、あるルートでの探索でN手以上かかって不詰と判断された局面が例えば別の詰み筋の変化の中に含まれていると「親局面も子局面も詰みが確定した不詰みの局面」が生じてしまいます。これを防ぐ簡単な方法としてはN手以上かかった、かつ、未だ探索されたことのない局面についてのみ不詰とするというものがあります。しかしこの方法も、詰将棋の各々の局面に到達するために掛かる手順は一通りではないという問題を根本的には解決できておらず、N手で詰まないということを厳密に証明することはできません。