高速な詰将棋アルゴリズムを完全に理解したい（ver2）

Qhapaq アドベント将棋記事7日目

※：連載記事ですが前回までの記事をmergeした記事になりますので過去作は読まなくても大丈夫です。

今の詰将棋アルゴリズムで最強と言われているハッシュテーブル+df-pn探索による詰将棋アルゴリズムの完全理解を目指していきます。今回はproof numberやハッシュテーブルなどの探索で用いられる単語の意味を説明します。

【proof numberとは】 proof numberとは平たく言えば詰将棋専用の盤面評価値みたいなものです。通常の盤面評価値と違って、詰み証明のための評価値(pn)と不詰証明のための評価値(dn)があります。pn、dnは「この局面の詰み/不詰を証明する為に調べなければならない局面の数」であり、値が小さいほど詰み/不詰に近いという扱いになります。そして、詰み /不詰が証明された局面についてはpn、dnは0になります。局面のpn、dn（厳密には非0のpn、dn）はあくまで探索途中での予測値にすぎないことに注意してください。即ち、pn、dnは探索の途中で増えたり減ったりします。

【ハッシュテーブルとは】雑に言えば局面毎のpn、dnを保存する辞書のようなものです。将棋などのゲームでは手順前後により重複した局面が多々でてくるため、一度探索した局面を覚えておくことで計算の効率を向上させます。

【proof numberの更新】ある局面のproof numberはその局面（親局面）から到達できる局面（子局面）のpn、dnを用いることで更新できます。各人が最善を尽くすという仮定により、攻める側の手番では「候補手の中でどれか一つでも詰みが見つかれば詰み」、「不詰を証明するには全ての手で不詰を証明しなければならない」という条件が、受ける側の手番では「候補手の中でどれか一つでも不詰が見つかれば良い」、「詰みを証明するには全ての手で詰みを証明しなければならない」となっていることに気をつけてください。即ち、pn、dnの更新方法はどちらの手番であるかによって変わります。

f:id:qhapaq:20200715082700p:plain — 攻める側の手番でのpn、dnの更新。pn、dnの値は仮のものです

f:id:qhapaq:20200715082750p:plain — 受ける側の手番でのpn、dnの更新。pn、dnの値は仮のものです。

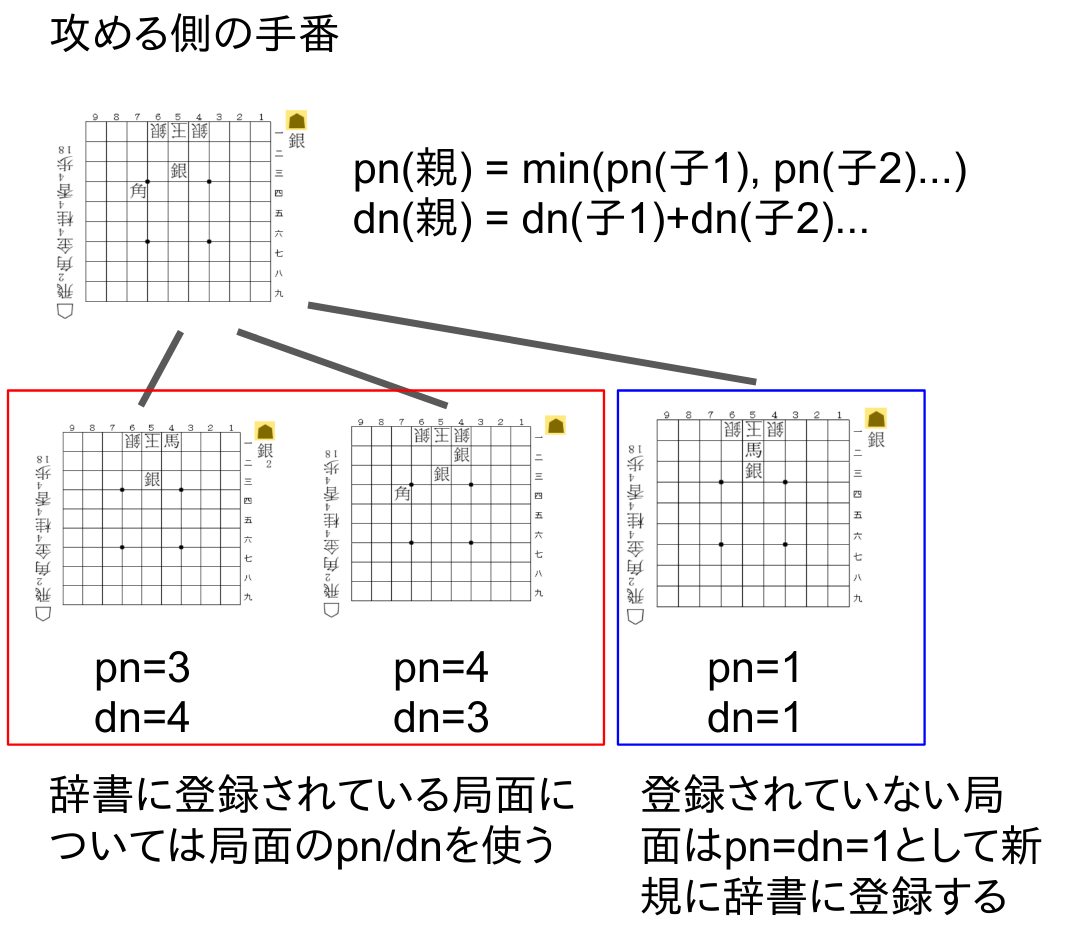
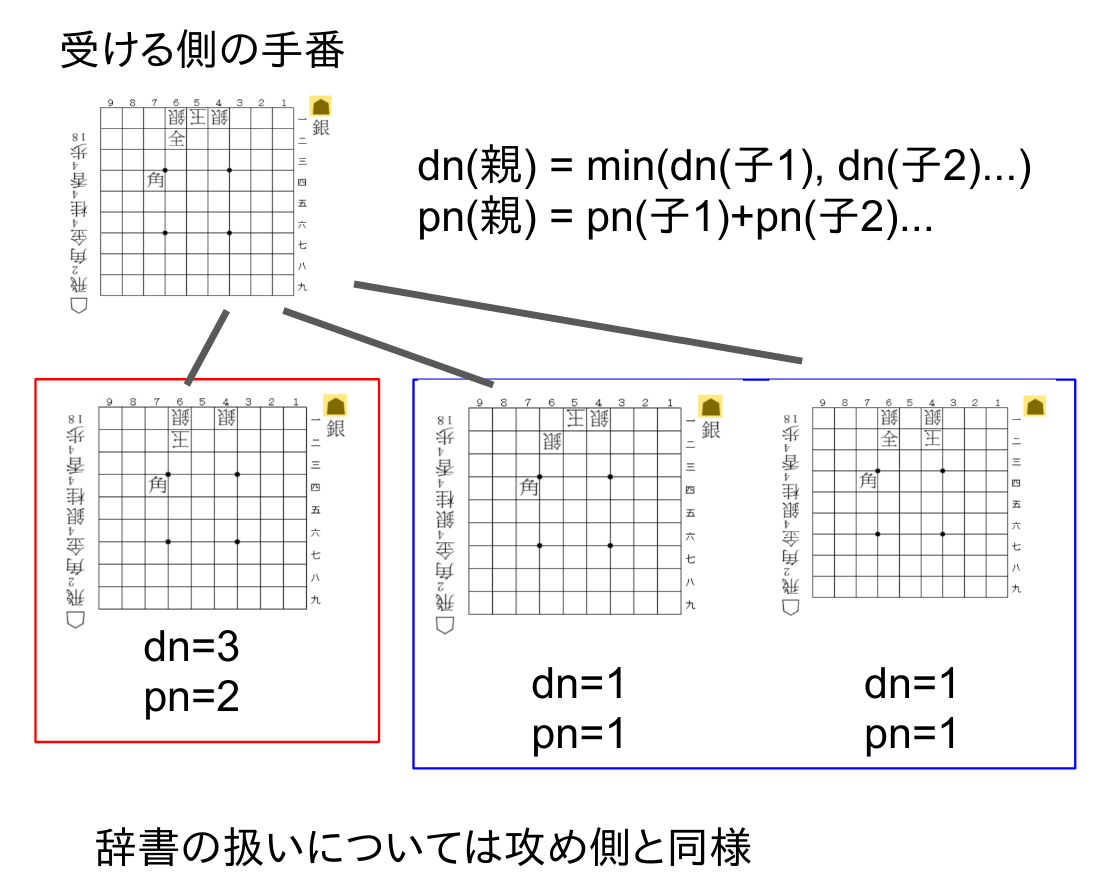
辞書の扱いにも注意してください。辞書に局面が記載されていない場合、pn=dn=1で初期化された状態で辞書に局面が追加されます。ハッシュテーブルを用いたdf-pn探索では各局面のpn,dnを逐次更新しながら、攻める側はできるだけ相手の受けが少ないような手（= 子局面のpnが小さいもの）を、受ける側はできるだけ次の王手が続きにくい手( = 子局面のdnが小さいもの)を優先して探索することで詰み、不詰みを高速に証明しようとしていっます。

今日はここまで。

【付録】 tanuki-の詰将棋エンジンに搭載されているアルゴリズムの原著論文（英語）の疑似コードに日本語の解説を付けたもの。コードが読める人だとこっちのほうが解りやすいかも。

func DFPNwithTCA(n, thpn, thdn, inc_flag) {

  // この関数が再帰的に呼ばれる。n=局面
  // thpn = n のproof number(pn)がこれ以上なら探索を打ち切る
  // thdn = nのdisproof number(dn)がこれ以上なら探索を打ち切る
  // inc_flag thpn, thdnを増やすことで探索を強制的に打ち切らないようにする

  // nが詰み、または、王手をかける手がない（不詰確定）の場合、探索を打ち切る
  if (n is a terminal node) {
    handle n 
    return;
   } 
   first time = true; // ループに入って最初の処理かを判別
   // 以下無限ループ
   while (1) {
      // n が探索されるのはこれが初めてならthpn, thdnの拡張は不要 
      if (n is a leaf) {
        inc flag = false;
      }
      // nの子局面の中にnよりも元局面からの深さが浅い局面がある = ループしている、かつ、子局面の詰み、不詰みが確定していない
      if (n has an unproven old child) {
        inc flag = true; // inc_flagをon
      }
      // 局面nから合法手を生成、子局面のpn, dnからnのpn,dnを計算する
      expand_and_compute_pn_dn(n);
      if (first time && inc flag) { 
        thpn = max(thpn, pn(n) + 1); 
        thdn = max(thdn, dn(n) + 1); 
      }
      // 局面nのpn, dnが thpn, thdnより多い
      // ≒局面nの兄弟局面の中にnよりpn, dnが小さい局面がある可能性がある
      if (pn(n) ≥ thpn || dn(n) ≥ thdn) break;
      first time= false; 
      // 局面nの子局面のなかでpn, dnが最も小さいもの、２番めに小さいものを探す
      n1, n2 = find_best_and_second_best_child(n);

      if (n is an OR node) { 
        // 攻め側の場合のpn, dnの更新
        thpn child = min(thpn, pn(n2) + 1); 
        thdn child = thdn - dn(n) + dn(n1);
      else { 
        // 受け側の場合の更新
        thpn child = thpn - pn(n) + pn(n1);
        thdn child = min(thdn, dn(n2) + 1);
     } 
     // 一番いい子ノードに対して再帰的に探索
     DFPNwithTCA(n1, thpn child, thdn child, inc flag); 
}